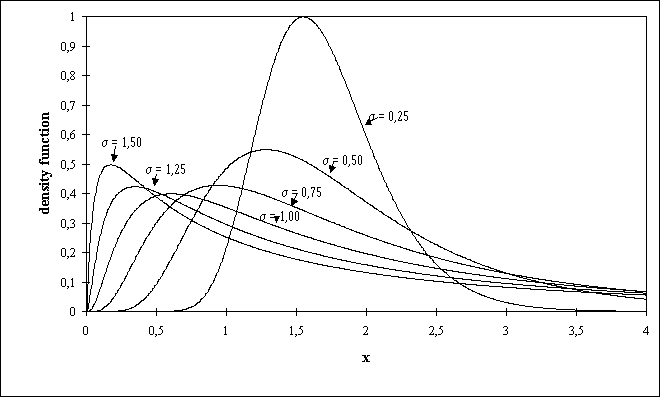
Figure 1: Behaviour of the logarithmical normal distribution by different standard deviations and constant mean value
| project sponsor: | German Research Foundation (DFG) |
| project leader: | Prof. (em.) Dr. Dr. H. Trumpold |
| project number: | Special Research Complex (SFB) 326, part P4 |
| researcher | Dipl.-Ing. C. Pertuch |
| research period | 01.01.1993 - 31.12.1998 |
In the current time there is a strong trend by all machines to go to
smaller and smaller. Because of this trend the dimensions and tolerances
of the component parts become also smaller and smaller. And therefore the
methods of precision machining becomes more and more importance, because
the demands for accuracy, safety, reliability and life span of the machines
becomes higher.
In the range of small and smallest dimensions and tolerances its necessary
not only to check the deviations of the measures but also the deviations
of the geo-metrical tolerances and the surface roughness.
Currently the process control is achieved by measurement of form, location
and roughness individually. With this measurement the results are only
checked against their tolerance limits. There are no control systems available,
that consider the statistical character of this one-side toleranced features.
The aim of this research projects its, to develop a control system for the moni-toring, the analysis and the control of this one side toleranced features. The investigations about this one side toleranced features were supported by grinding examples of the deviations from roundness, from parallelism, from straightness and of the parameters of surface roughness. For that purpose measurements were made of a process in a factory and in our own experimental workshop. The results of our investigations shown clearly, that the model distributions of one side toleranced geometrical features can not described through a normal distribution.
The best description for the whole distribution of the deviation from
roundness and of the parameters of surface roughness Rz and Rmax are often
the logarithmical normal distribution. The behaviour of the logarithmical
normal distribution in the cases of different standard deviations are shown
in figure 1. For the values of roundness deviation and Rz an approximation
with a normal distribu-tion is possible.
 |
Figure 1: Behaviour of the logarithmical normal distribution by different standard deviations and constant mean value |
The deviation from parallelism can be described best with the transformed
logarithmical normal distribution and the transformed normal distribution.
The deviation from straightness can be described best with the folded
normal distribution (figure 2). A approximation with the transformed logarithmical
normal distribution and the transformed normal distribution are possible.
 |
Figure 2: regression coefficients for deviation of straightness of side 1 |
The actual work are occupied with theoretical investigations about the basics of possible model distributions. Interesting are the folded normal distribution, which describe the distributions of the measuring values closely.
To achieve generally accepted results, further investigations should be done in team-work with other parts of SFB 326 and with a greater number of techno-logical parameters and with more parameters of geometrical features.
Letzte Änderung: 10. März 2000
Anmerkungen an: carsten@pertuch.de